UGC NET Exam Date 2020 Released. Check revised exam dates at Official Website ugcnet.nta.nic.in

University Grants Commission – National Eligibility Test (UGC-NET)

UGC NET 2020 Exam Dates Postponed for below subjects

• Assamese, Malayalam, Marathi, Punjabi, Russian, Telugu, Bengali, Bodo, Kashmiri, Social Medicine & Community Health, Urdu postponed to date November 04, 2020
• Computer Science, Sociology postponed to date November 11, 2020
• Education, Geography postponed to date November 12, 2020
• Hindi postponed to date November 13, 2020

NTA UGC NET Exam June 2020 revised date sheet announced, Admit card displayed at Official Website @ugcnet.nta.nic.in

(UGC-NET) : June 2020 Date Sheet of Examination

The UGC-NET June 2020 will be held as per following Schedule. Admit Cards for the examination to be held on 24.09.2020 and 25.09.2020 have been displayed. For others same shall be displayed on the NTA website soon.

NTA UGC NET 2020 Revised Exam Dates

Date	Time	Subject Code	Subject Name	Remark
September 24, 2020	09.00AM to 12.00 Noon (IST)	46	Adult Education/ Continuing Education/ Andragogy/ Non Formal Education.
		32	Chinese
		62	Comparative Study of Religions
		33	Dogri
		44	German
		37	Gujarati
		50	Indian Culture
		45	Japanese
		21	Kannada
		85	Konkani
		18	Maithili
		35	Manipuri
		42	Persian
		91	Prakrit
		43	Rajasthani
		25	Sanskrit
		101	Sindhi
		40	Spanish
		70	Tribal and Regional Language/Literature
	03.00PM to 06.00PM (IST)	49	Arab Culture and Islamic Studies
		29	Arabic
		60	Buddhist, Jaina, Gandhian and Peace Studies
		11	Defence and Strategic Studies
		31	Linguistics
		63	Mass Communication and Journalism
		34	Nepali
		23	Oriya
		83	Pali
		26	Tamil
September 25, 2020	09.00AM to 12.00 Noon (IST)	72	Comparative Literature
		68	Criminology
		71	Folk Literature
		82	Forensic Science
		39	French (French Version)
		66	Museology & Conservation
		4	Psychology
		93	Tourism Administration and Management.
	03.00PM to 06.00PM (IST)	67	Archaeology
		92	Human Rights and Duties
		59	Library and Information Science
		3	Philosophy
		90	Politics including International Relations/International Studies including Defence/Strategic Studies, West Asian Studies, South East Asian Studies, African Studies,South Asian Studies, Soviet Studies, American Studies.
September 29, 2020	09.00AM to 12.00 Noon (IST)	58	Law
		47	Physical Education
	03.00PM to 06.00PM (IST)	89	Environmental Sciences
		65	Performing Art - Dance/Drama/Theatre
		73	Sanskrit traditional subjects (including) Jyotisha/Sidhanta Jyotish/ Navya Vyakarna/ Vyakarna/ Mimansa/ Navya Nyaya/ Sankhya Yoga/ Tulanatmaka Darsan/ Shukla Yajurveda/ Madhav Vedant/ Dharmasasta/ Sahitya/Puranotihasa /
		95	Santali
		74	Women Studies
September 30, 2020	09.00AM to 12.00 Noon (IST)	17	Management (including Business Admn. Mgt./Marketing/ Marketing Mgt./Industrial Relations and Personnel Mgt./Personnel Mgt./Financial Mgt./Co-operative Management)
September 30, 2020	03.00PM to 06.00PM (IST)	1	Economics / Rural Economics /Co-operation / Demography / Development Planning/ Development Studies / Econometrics/ Applied Economics/DevelopmentEco./Business Economics
October 1, 2020	09.00AM to 12.00 Noon (IST)	030	English	Group-1
	03.00PM to 06.00PM (IST)			Group-2
October 9, 2020	09.00AM to 12.00 Noon (IST)	6	History
	03.00PM to 06.00PM (IST)	2	Political Science
October 17, 2020	09.00AM to 12.00 Noon (IST)	008	Commerce	Group-1
	03.00PM to 06.00PM (IST)			Group-2
November 04, 2020(Old Date:22.10.2020)	09.00AM to 12.00 Noon (IST)	36	Assamese
		22	Malayalam
		38	Marathi
		24	Punjabi
		41	Russian
		27	Telugu
	03.00PM to 06.00PM (IST)	19	Bengali
		28	Urdu
		94	Bodo
		84	Kashmiri
		81	Social Medicine & Community Health
November 5, 2020	09.00AM to 12.00 Noon (IST)	88	Electronic Science
		55	Labour Welfare/Personnel Management/Industrial Relations/ Labour and Social Welfare/Human Resource Management
		16	Music
		15	Population Studies
		79	Visual Art (including Drawing & Painting/Sculpture Graphics/Applied Art/History of Art)
	03.00PM to 06.00PM (IST)	7	Anthropology
		12	Home Science
		14	Public Administration
		10	Social Work
		100	Yoga
November 11, 2020 (Old Date:07.10.2020)	09.00AM to 12.00 Noon (IST)	5	Sociology
	03.00PM to 06.00PM (IST)	87	Computer Science and Applications
November 12, 2020 (Old Date : 21.10.2020)	09.00AM to 12.00 Noon (IST)	9	Education
	03.00PM to 06.00PM (IST)	80	Geography
November 13, 2020 (Old Date:23.10.2020)	09.00AM to 12.00 Noon (IST)	020	Hindi	Group-1
	03.00PM to 06.00PM (IST)			Group-2

NTA UGC NET - June 2020 Exam Dates Postponed
(14th September, 2020 Public Notice) (Old Notice) :

This notice is regarding the postponed exam dates for NTA UGC NET - June 2020 Exam

National Testing Agency, NTA has released a notice informing that the UGC NET Exam 2020 has been postponed to be conducted now from September 24, 2020, onwards. The candidates who were to appear for the exam from September 16 must note that now the exams have been postponed by a week. The downloading of the admit card will soon be released on ugc.nta.nic.in.

Visit Official Website and check updates in section LATEST @ NTA with subject "Conduct of UGC- NET June Examination, 2020.":


Public Notice by NTA for UGC NET Examination (notice date: 14th September 2020)


National Testing Agency will be conducting ICAR Examination AIEEA-UG/PG and AICE-JRF/SRF (Ph.D.) 2020-21 on 16, 17, 22 and 23 September 2020. In view of ICAR Examination AIEEA-UG/PG and AICE-JRF/SRF (Ph.D.) 2020-21 being conducted on the above mentioned dates, UGC - NET 2020 Examination will now be held from 24th September onwards, this is due to some common candidates in both exams and the requests received thereof. The exact schedule of Subject-wise and Shift-wise details will be uploaded subsequently. The downloading of Admit Cards indicating Roll Number, Examination Centre, Date, Shift and timing of Examination will be announced shortly on the official website (ugcnet.nta.nic.in) of UGC- NET Examination, 2020.


Last Month updates
NTA Exam Dates 2020 Updates : Schedule for UGC NET Exam released at official website Auguest Updates from NTA NET regarding the Exam dates : Final date for UGC NET June exam announced on Thursday, 20 August, 2020.

Visit and check Exam date updates at UGC NET official website:

Public Notice by NTA for UGC NET Examination

UGC NET Exam date :
UGC - National Eligibility Test (UGC NET) June 2020 will be conducated in September on dates (16-18) Sep, 2020 and (21-25) Sep, 2020.

Downloading of Admit Cards:
The downloading of Admit Cards indicating Roll Number, Centre, Date, Shift and timing of Examination, will commence about 15 days before the date of examination on the respective official websites of these examinations

NTA UGC NET Computer Science | Graph Theory Questions Set 1 | Discrete Structures and Optimization

Question 1

---

The number of different spanning trees in complete graph, K4 and bipartite graph, K2,2 have ______ and _______ respectively.

1. 1. 14, 14
2. 2. 16, 14
3. 3. 16, 4
4. 4. 14, 4

Explanation Question 1

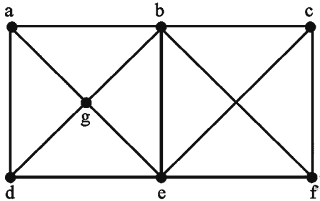
For any complete graph K_n with n nodes, different spanning trees possible is n^(n-2)
So, spanning trees in complete graph K4 will be 4^{(4 - 2)}.
i.e. 4² = 16.

For any Bipartite graph K_m,n with m and n nodes, different spanning trees possible is
m^(n-1).n^(m-1)
So, spanning trees in K_2,2 will be 2^(2-1) * 2^(2-1).
i.e. 2 * 2 = 4.

So, option 3 is correct answer.

Question 2

---

A clique in a simple undirected graph is a complete subgraph that is not contained in any larger complete subgraph. How many cliques are there in the graph shown below?

1. 1. 2
2. 2. 4
3. 3. 5
4. 4. 6

Explanation Question 2

Total 5 clique will be there.
So, option (C) is correct.

Question 3

---

Which of the following statement(s) is/are false ?
(a) A connected multigraph has an Euler Circuit if and only if each of its vertices has even degree.
(b) A connected multigraph has an Euler Path but not an Euler Circuit if and only if it has exactly two vertices of odd degree.
(c) A complete graph (Kn) has a Hamilton Circuit whenever n ≥ 3.
(d)A cycle over six vertices (C6) is not a bipartite graph but a complete graph over 3 vertices is bipartite.
Codes:

1. 1. (a) only
2. 2. (b) and (c)
3. 3. (c) only
4. 4. (d) only

Explanation Question 3

A connected multigraph has an Euler Circuit if and only if each of its vertices has even degree.Correct A connected multigraph has an Euler Path but not an Euler Circuit if and only if it has exactly two vertices of odd degree.Correct A complete graph (Kn) has a Hamilton Circuit whenever n ≥ 3.CorrectA cycle over six vertices (C6) is not a bipartite graph but a complete graph over 3 vertices is bipartite.Incorrect
So, option (D) is cocrrect.

Question 4

---

Consider the graph given below:

The two distinct sets of vertices, which make the graph bipartite are:

1. 1. (v1, v4, v6); (v2, v3, v5, v7, v8)
2. 2. (v1, v7, v8); (v2, v3, v5, v6)
3. 3. (v1, v4, v6, v7); (v2, v3, v5, v8)
4. 4. (v1, v4, v6, v7, v8); (v2, v3, v5)

Explanation Question 4

A Bipartite Graph is a graph whose vertices can be divided into two independent sets, U and V such that every edge (u, v) either connects a vertex from U to V or a vertex from V to U. In other words, for every edge (u, v), either u belongs to U and v to V, or u belongs to V and v to U. We can also say that there is no edge that connects vertices of same set.
(v1, v4, v6, v7);
(v2, v3, v5, v8) is a bipartite graph vertices set.
So, option (C) is correct.

Question 5

---

A tree with n vertices is called graceful, if its vertices can be labelled with integers 1, 2,....n such that the absolute value of the difference of the labels of adjacent vertices are all different. Which of the following trees are graceful?

codes:

1. 1. (a) and (b)
2. 2. (b) and (c)
3. 3. (a) and (c)
4. 4. (a), (b) and (c)

Explanation Question 5

All given trees are graceful.
So, option (D) is correct.

Question 6

---

In the following graph, discovery time stamps and finishing time stamps of Depth First Search (DFS) are shown as x/y, where x is discovery time stamp and y is finishing time stamp. It shows which of the following depth first forest?

1. 1. {a, b, e} {c, d, f, g, h}
2. 2. {a, b, e} {c, d, h} {f, g}
3. 3. {a, b, e} {f, g} {c, d} {h}
4. 4. {a, b, c, d} {e, f, g} {h}

Explanation Question 6

Question 7

---

The inorder traversal of the following tree is:

1. 1. 2 3 4 6 7 13 15 17 18 18 20
2. 2. 20 18 18 17 15 13 7 6 4 3 2
3. 3. 15 13 20 4 7 17 18 2 3 6 18
4. 4. 2 4 3 13 7 6 15 17 20 18 18

Explanation Question 7

In inorder traversal first we traverse left node then root node and then right node: In the following tree we first go to the leftmost node then its root after that right i.e. 2 4 3 13 7 6 15 17 20 18 18. In rest of the option inorder property is violating. So, option (D) is correct.

Question 8

---

Consider the following statements:
(a) Depth - first search is used to traverse a rooted tree.
(b) Pre - order, Post-order and Inorder are used to list the vertices of an ordered rooted tree.
(c) Huffman's algorithm is used to find an optimal binary tree with given weights.
(d) Topological sorting provides a labelling such that the parents have larger labels than their children.
Which of the above statements are true?

1. 1. (a) and (b)
2. 2. (c) and (d)
3. 3. (a), (b) and (c)
4. 4. (a), (b), (c) and (d)

Explanation Question 8

Depth - first search is used to traverse a rooted tree. Correct Pre - order, Post-order and Inorder are used to list the vertices of an ordered rooted tree. CorrectHuffman's algorithm is used to find an optimal binary tree with given weights. CorrectTopological sorting provides a labelling such that the parents have larger labels than their children.Correct
So, option (D) is correct.

Question 9

---

Consider a Hamiltonian Graph (G) with no loops and parallel edges. Which of the following is true with respect to this Graph (G) ?
(a) deg (v) ≥ n / 2 for each vertex of G
(b) |E(G)| ≥ 1 / 2 (n - 1) (n - 2) + 2 edges
(c) deg (v) + deg (w) ≥ n for every n and v not connected by an edge.

1. 1. (a) and (b)
2. 2. (b) and (c)
3. 3. (a) and (c)
4. 4. (a), (b) and (c)

Explanation Question 9

In an Hamiltonian Graph (G) with no loops and parallel edges:
According to Dirac's theorem in a n vertex graph, deg (v) ≥ n / 2 for each vertex of G.
According to Ore's theorem deg (v) + deg (w) ≥ n for every n and v not connected by an edge is sufficient condition for a graph to be hamiltonian.
If |E(G)| ≥ 1 / 2 * [(n - 1) (n - 2)] then graph is connected but it doesn't guaranteed to be Hamiltonian Graph.
(a) and (c) is correct regarding to Hamiltonian Graph.
So, option (C) is correct.

Question 10

---

Consider the given graph

Its Minimum Cost Spanning Tree is __________.

(1)
(2)
(3)
(4)

1. 1. (1)
2. 2. (2)
3. 3. (3)
4. 4. (4)

Explanation Question 10

A minimum spanning tree (MST) or minimum weight spanning tree for a weighted, connected and undirected graph is a spanning tree with weight less than or equal to the weight of every other spanning tree.
In option (A) weight of tree is = 103 but it is not the subgraph from graph because in original graph there is no edge between node(6) and (7).
In option (B) weight of tree is = 99
In option (C) weight of tree is = 127
In option (D) weight of tree is = 106
So, option (B) is correct.