NTA UGC NET Computer Science | Graph Theory Questions Set 1 | Discrete Structures and Optimization

Question 1

---

The number of different spanning trees in complete graph, K4 and bipartite graph, K2,2 have ______ and _______ respectively.

1. 1. 14, 14
2. 2. 16, 14
3. 3. 16, 4
4. 4. 14, 4

Explanation Question 1

For any complete graph K_n with n nodes, different spanning trees possible is n^(n-2)
So, spanning trees in complete graph K4 will be 4^{(4 - 2)}.
i.e. 4² = 16.

For any Bipartite graph K_m,n with m and n nodes, different spanning trees possible is
m^(n-1).n^(m-1)
So, spanning trees in K_2,2 will be 2^(2-1) * 2^(2-1).
i.e. 2 * 2 = 4.

So, option 3 is correct answer.

Question 2

---

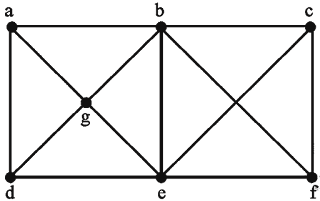
A clique in a simple undirected graph is a complete subgraph that is not contained in any larger complete subgraph. How many cliques are there in the graph shown below?

1. 1. 2
2. 2. 4
3. 3. 5
4. 4. 6

Explanation Question 2

Total 5 clique will be there.
So, option (C) is correct.

Question 3

---

Which of the following statement(s) is/are false ?
(a) A connected multigraph has an Euler Circuit if and only if each of its vertices has even degree.
(b) A connected multigraph has an Euler Path but not an Euler Circuit if and only if it has exactly two vertices of odd degree.
(c) A complete graph (Kn) has a Hamilton Circuit whenever n ≥ 3.
(d)A cycle over six vertices (C6) is not a bipartite graph but a complete graph over 3 vertices is bipartite.
Codes:

1. 1. (a) only
2. 2. (b) and (c)
3. 3. (c) only
4. 4. (d) only

Explanation Question 3

A connected multigraph has an Euler Circuit if and only if each of its vertices has even degree.Correct A connected multigraph has an Euler Path but not an Euler Circuit if and only if it has exactly two vertices of odd degree.Correct A complete graph (Kn) has a Hamilton Circuit whenever n ≥ 3.CorrectA cycle over six vertices (C6) is not a bipartite graph but a complete graph over 3 vertices is bipartite.Incorrect
So, option (D) is cocrrect.

Question 4

---

Consider the graph given below:

The two distinct sets of vertices, which make the graph bipartite are:

1. 1. (v1, v4, v6); (v2, v3, v5, v7, v8)
2. 2. (v1, v7, v8); (v2, v3, v5, v6)
3. 3. (v1, v4, v6, v7); (v2, v3, v5, v8)
4. 4. (v1, v4, v6, v7, v8); (v2, v3, v5)

Explanation Question 4

A Bipartite Graph is a graph whose vertices can be divided into two independent sets, U and V such that every edge (u, v) either connects a vertex from U to V or a vertex from V to U. In other words, for every edge (u, v), either u belongs to U and v to V, or u belongs to V and v to U. We can also say that there is no edge that connects vertices of same set.
(v1, v4, v6, v7);
(v2, v3, v5, v8) is a bipartite graph vertices set.
So, option (C) is correct.

Question 5

---

A tree with n vertices is called graceful, if its vertices can be labelled with integers 1, 2,....n such that the absolute value of the difference of the labels of adjacent vertices are all different. Which of the following trees are graceful?

codes:

1. 1. (a) and (b)
2. 2. (b) and (c)
3. 3. (a) and (c)
4. 4. (a), (b) and (c)

Explanation Question 5

All given trees are graceful.
So, option (D) is correct.

Question 6

---

In the following graph, discovery time stamps and finishing time stamps of Depth First Search (DFS) are shown as x/y, where x is discovery time stamp and y is finishing time stamp. It shows which of the following depth first forest?

1. 1. {a, b, e} {c, d, f, g, h}
2. 2. {a, b, e} {c, d, h} {f, g}
3. 3. {a, b, e} {f, g} {c, d} {h}
4. 4. {a, b, c, d} {e, f, g} {h}

Explanation Question 6

Question 7

---

The inorder traversal of the following tree is:

1. 1. 2 3 4 6 7 13 15 17 18 18 20
2. 2. 20 18 18 17 15 13 7 6 4 3 2
3. 3. 15 13 20 4 7 17 18 2 3 6 18
4. 4. 2 4 3 13 7 6 15 17 20 18 18

Explanation Question 7

In inorder traversal first we traverse left node then root node and then right node: In the following tree we first go to the leftmost node then its root after that right i.e. 2 4 3 13 7 6 15 17 20 18 18. In rest of the option inorder property is violating. So, option (D) is correct.

Question 8

---

Consider the following statements:
(a) Depth - first search is used to traverse a rooted tree.
(b) Pre - order, Post-order and Inorder are used to list the vertices of an ordered rooted tree.
(c) Huffman's algorithm is used to find an optimal binary tree with given weights.
(d) Topological sorting provides a labelling such that the parents have larger labels than their children.
Which of the above statements are true?

1. 1. (a) and (b)
2. 2. (c) and (d)
3. 3. (a), (b) and (c)
4. 4. (a), (b), (c) and (d)

Explanation Question 8

Depth - first search is used to traverse a rooted tree. Correct Pre - order, Post-order and Inorder are used to list the vertices of an ordered rooted tree. CorrectHuffman's algorithm is used to find an optimal binary tree with given weights. CorrectTopological sorting provides a labelling such that the parents have larger labels than their children.Correct
So, option (D) is correct.

Question 9

---

Consider a Hamiltonian Graph (G) with no loops and parallel edges. Which of the following is true with respect to this Graph (G) ?
(a) deg (v) ≥ n / 2 for each vertex of G
(b) |E(G)| ≥ 1 / 2 (n - 1) (n - 2) + 2 edges
(c) deg (v) + deg (w) ≥ n for every n and v not connected by an edge.

1. 1. (a) and (b)
2. 2. (b) and (c)
3. 3. (a) and (c)
4. 4. (a), (b) and (c)

Explanation Question 9

In an Hamiltonian Graph (G) with no loops and parallel edges:
According to Dirac's theorem in a n vertex graph, deg (v) ≥ n / 2 for each vertex of G.
According to Ore's theorem deg (v) + deg (w) ≥ n for every n and v not connected by an edge is sufficient condition for a graph to be hamiltonian.
If |E(G)| ≥ 1 / 2 * [(n - 1) (n - 2)] then graph is connected but it doesn't guaranteed to be Hamiltonian Graph.
(a) and (c) is correct regarding to Hamiltonian Graph.
So, option (C) is correct.

Question 10

---

Consider the given graph

Its Minimum Cost Spanning Tree is __________.

(1)
(2)
(3)
(4)

1. 1. (1)
2. 2. (2)
3. 3. (3)
4. 4. (4)

Explanation Question 10

A minimum spanning tree (MST) or minimum weight spanning tree for a weighted, connected and undirected graph is a spanning tree with weight less than or equal to the weight of every other spanning tree.
In option (A) weight of tree is = 103 but it is not the subgraph from graph because in original graph there is no edge between node(6) and (7).
In option (B) weight of tree is = 99
In option (C) weight of tree is = 127
In option (D) weight of tree is = 106
So, option (B) is correct.